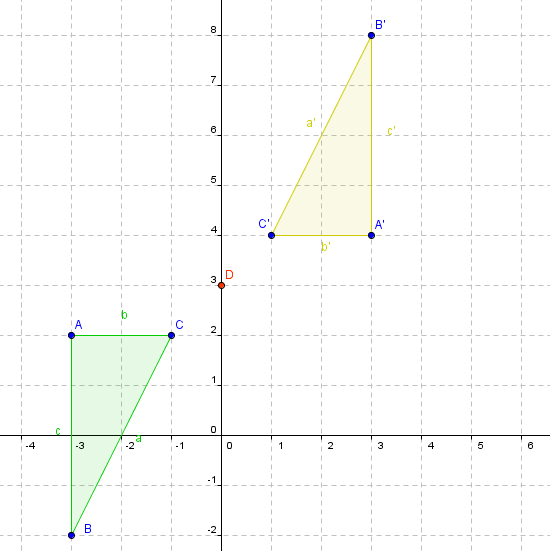
Transformaciones Isométricas -Básica- Las transformaciones isométricas son cambios de posición (orientación) de una figura determinada que NO alteran la forma ni el tamaño de ésta.
Entre las transformaciones Isométricas están las Traslaciones, Rotaciones y Reflexiones (o simetrias), que serán vistas a continuación, y cuyo estudio será pieza fundamental para la posterior comprensión de las teselaciones o embaldosados.
1) Traslaciones: Son aquellas isometrías que permiten desplazar en línea recta todos los puntos del plano. Este desplazamiento se realiza según un "vector de traslación dado".
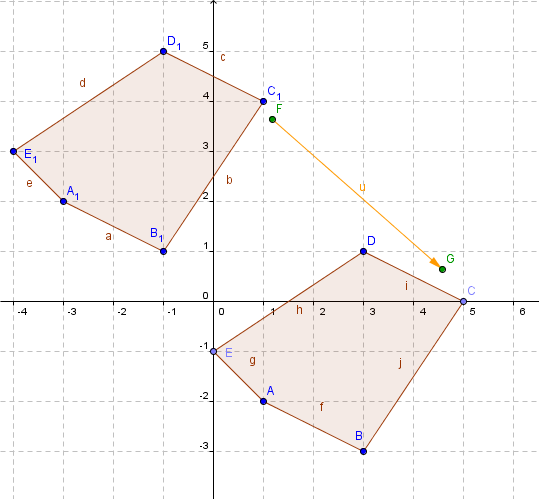
2) Rotaciones: Son aquellas isometrías que permiten girar todos los puntos del plano. Cada punto gira siguiendo un arco que tiene un centro y un ángulo determinados, por lo que toda rotación queda definida por su centro de rotación y por su ángulo de giro. Si se efectua en sentido contrario a como giran las manecillas del reloj, se dice positiva; de lo contrario, negativa u horaria.
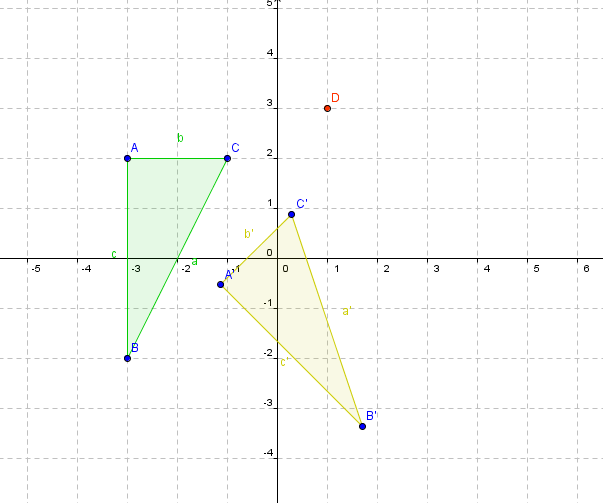
(En esta imágen podemos ver una rotación del triángulo ABC, con respecto al punto D, de 45°.)
3) Simetrias: Las simetrias o reflexiones son aquellas transformaciones que invierten los puntos y figuras del plano (como si los reflejáramos con un espejo). Pueden ser respecto a un punto (Central), o a una recta (Axial).
a) Simetria Central: Dado un punto cualquiera fijo P del plano, se llama simetria central con respecto P, a aquella isometria que lleva cada punto A del plano a una posición A´, de modo que A´ está en la recta PA, a distinto lado con respecto a P, y AP = A´P. El punto P se llama centro de simetria, y A y A´, puntos correspondientes u homólogos.
b) Simetria Axial: Dada una recta fija L del plano, se llama simetria axial (o reflexión) con respecto L, a aquella isometría tal que, si P y P´ son puntos homóloggos con respecto a ella, PP´ es perpendicular a L y, además, el punto medio de PP´ está en L.
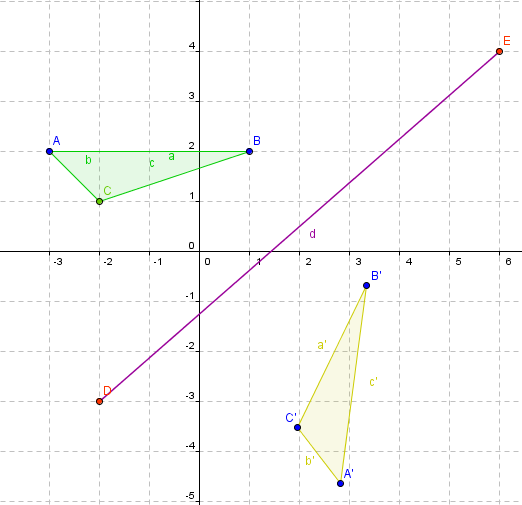
En el siguiente video puedes ver como efectuar estas transformaciones con geogebra