Curso gratis de Geometria de Séptimo básico a Primero medio
Perfilado de sección
-
Geometría - Séptimo básico a Primero medio-
-
Geometría de Séptimo básico a Primero Medio
Este curso busca que los jóvenes puedan nivelar conocimientos relacionados al área de geometría, y aclaren dudas de una manera gratuita y amena, utilizandolo como un complemento para sus estudios si así se desea; estará dividido en tres unidades fundamentales, cuyos contenidos corresponden a séptimo, octavo básico y primero medio.
La primera unidad ofrece a los estudiantes la posibilidad de resolver desafios que estimulen el pensamiento y la imaginación, a través de las construcciones geométricas con regla y compás o un procesador geométrico; esta unidad se inicia con los trazados fundamentales en el plano (que son las bases de las construcciones), se caracterizan los elementos lineales de los triángulos, se comprueban algunas de sus propiedades, y se construyen a partir de las medidas de sus lados y/o ángulos.
En la segunda unidad, los estudiantes conocerán las transformaciones isométricas, aprenderán el concepto de lugar geométrico y calcularán áreas de círculos y figuras tridimensionales, perímetro en la circunferencia, y volúmenes en figuras tridimensionales.
En este punto se puede integrar la geometría con las artes plásticas, pues aprenderán a construir teselaciones, conocerán el número pi, profundizarán sus conocimientos acerca de figuras tridimensionales (como el cono, el cilindro y la pirámide) y ampliarán su lenguaje geométrico mediante el trabajo con lugares geométricos.
Por último, la tercera unidad ofrece a los alumnos la posibilidad de trabajar la geometría en el plano cartesiano, donde estudiarán las transformaciones isométricas y la congruencia de figuras.
Específicamente, los estudiantes trabajan los elementos básicos del plano cartesiano, transforman figuras del plano a través de la aplicación de traslaciones, rotaciones y reflexiones, desarrollan el concepto de congruencia a partir del concepto de transformación isométrica, establecen los criterios de congruencia en triángulos, y los utilizan en la resolución de problemas y en el establecimiento de propiedades en polígonos.
Espero que este curso les sea de Utilidad; y ahora que ya se ha introducido en el tema, ¡podemos comenzar!
-
Al aprobar esta evaluación, se habilitará el sistema para la descarga del certificado. Podrás descargar cualquiera o los tres modelos de certificado en cuanto apruebas la evaluación.
-
-
Antes de comenzar... Geogebra!!
-
Ya que es más complicado realizar estas actividades de forma manual, utilizaremos un programa de Geometria Dinámica llamado "Geogebra", el que se puede descargar en el siguiente link: http://www.geogebra.org/cms/es/download/. Selecciona la opción que necesites, se descargará automáticamente; sigue los pasos, y luego de unos minutos, deberias poder utilizarlo
Parte viendo este video (si quieres empieza a verlo desde el minuto 1.50, ya que el resto es sobre instalación) en el que enseñan a utilizar Geogebra de manera básica:
Pero, si quieres profundizar en el tema, puedes visitar otro curso de Educagratis dictado por el Dr. Pedro Salcedo Lagos: http://www.educagratis.org/moodle/course/view.php?id=67.
Y ahora estamos en condiciones de empezar!!
-
-
Esta unidad se inicia con los trazados fundamentales en el plano (que son las bases de las construcciones), como las perpendiculares, paralelas, bisectrices, y la copia de segmentos y ángulos. Se caracterizan los elementos lineales de los triángulos y se comprueban algunas de sus propiedades. Se construyen triángulos a partir de las medidas de sus lados y/o ángulos, y se construyen ángulos utilizando regla y compás o un procesador geométrico.
Conocimientos previos:
› Rectas paralelas y perpendiculares
› Bisectrices, alturas, transversales de gravedad, simetrales
› Ángulos agudos, rectos y obtusos
› Triángulos según sus lados y según sus ángulos
Puedes revisar la construcción de éstos elementos en el siguiente video
-
Apertura: jueves, 3 de octubre de 2013, 17:55Cierre: jueves, 10 de octubre de 2013, 17:55
-
Construcciones Geométricas: parte 2
Elementos de los tríangulos
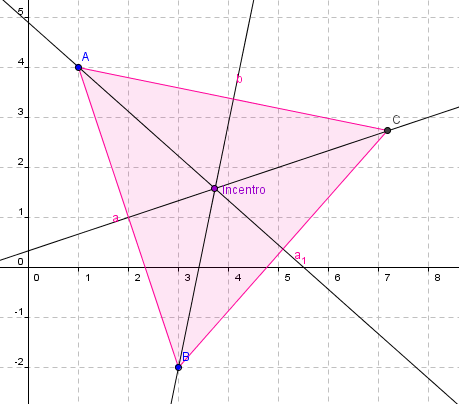
Bisectriz es la semirrecta que divide a un ángulo en dos partes iguales.
Incentro es el punto de intersección de las tres bisectrices de un triángulo. Es el centro de la circunferencia inscripta.
Mediatriz de un segmento es la recta perpendicular al mismo en su punto medio.
Circuncentro es el punto de intersección de las tres mediatrices de un triángulo. Es el centro de la circunferencia circunscripta.
Altura es el segmento perpendicular comprendido entre un vértice y el lado opuesto.
Ortocentro es el punto de intersección de las tres alturas de un triángulo.
Mediana es el segmento comprendido entre un vértice y el punto medio del lado opuesto.
Baricentro es el punto de intersección de las tres medianas de un triángulo.
Además, te aconsejo que revises esta página, en la que describen clara y detalladamente la clasificación y algunas propiedades de los diferentes tipos de triángulos:
http://www.sangakoo.com/es/temas/clasificacion-y-propiedades-de-los-triangulos.-
Apertura: martes, 5 de noviembre de 2013, 18:45Cierre: martes, 12 de noviembre de 2013, 18:45
-
Ahora avanzamos a los contenidos de Octavo básico
Perímetro, área y volúmen:En este capítulo estudiaremos las transformaciones isométricas, se conocerá el concepto de lugar geométrico y calcularemos áreas en el círculo, perímetros en la circunferencia y áreas y volúmenes en figuras tridimensionales.
Contenidos:
- Vectores en el plano
- Ejes de Simetria
- Traslaciones, Rotaciones y Reflexiones
- Teselaciones
- Perímetro de la Circunferencia
- Área del círculo
- Áreas de la superficie de conos, cilindros y pirámides.
- Volúmenes de conos, cilindros y pirámides.
Puedes comenzar revisando este video, en el que se explica claramente como calular áreas de figuras planas: -
Transformaciones Isométricas -Básica-
Las transformaciones isométricas son cambios de posición (orientación) de una figura determinada que NO alteran la forma ni el tamaño de ésta.
Entre las transformaciones Isométricas están las Traslaciones, Rotaciones y Reflexiones (o simetrias), que serán vistas a continuación, y cuyo estudio será pieza fundamental para la posterior comprensión de las teselaciones o embaldosados.
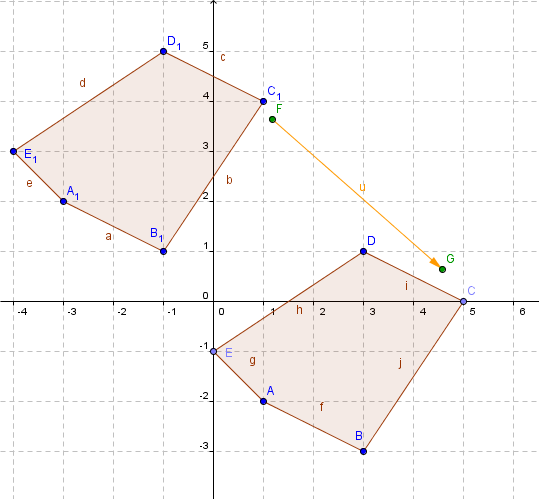
1) Traslaciones: Son aquellas isometrías que permiten desplazar en línea recta todos los puntos del plano. Este desplazamiento se realiza según un "vector de traslación dado".
2) Rotaciones: Son aquellas isometrías que permiten girar todos los puntos del plano. Cada punto gira siguiendo un arco que tiene un centro y un ángulo determinados, por lo que toda rotación queda definida por su centro de rotación y por su ángulo de giro. Si se efectua en sentido contrario a como giran las manecillas del reloj, se dice positiva; de lo contrario, negativa u horaria.
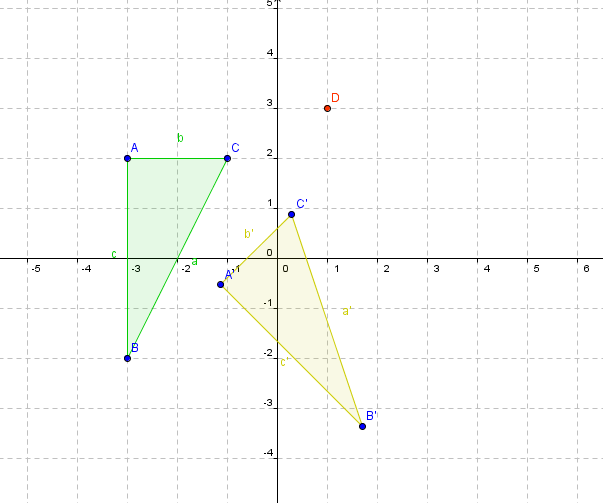
(En esta imágen podemos ver una rotación del triángulo ABC, con respecto al punto D, de 45°.)
3) Simetrias: Las simetrias o reflexiones son aquellas transformaciones que invierten los puntos y figuras del plano (como si los reflejáramos con un espejo). Pueden ser respecto a un punto (Central), o a una recta (Axial).
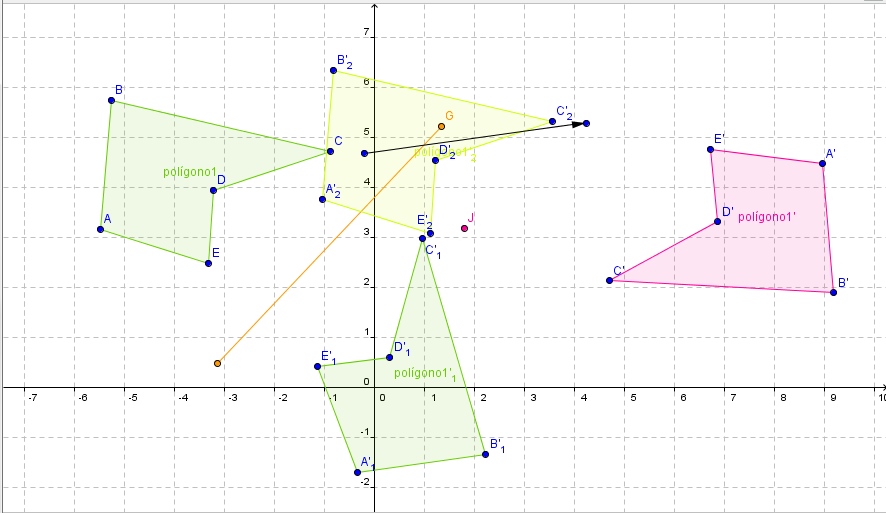
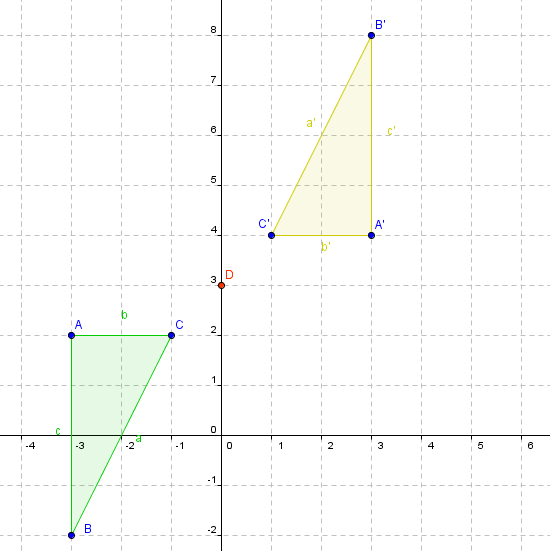
a) Simetria Central: Dado un punto cualquiera fijo P del plano, se llama simetria central con respecto P, a aquella isometria que lleva cada punto A del plano a una posición A´, de modo que A´ está en la recta PA, a distinto lado con respecto a P, y AP = A´P. El punto P se llama centro de simetria, y A y A´, puntos correspondientes u homólogos.
b) Simetria Axial: Dada una recta fija L del plano, se llama simetria axial (o reflexión) con respecto L, a aquella isometría tal que, si P y P´ son puntos homóloggos con respecto a ella, PP´ es perpendicular a L y, además, el punto medio de PP´ está en L.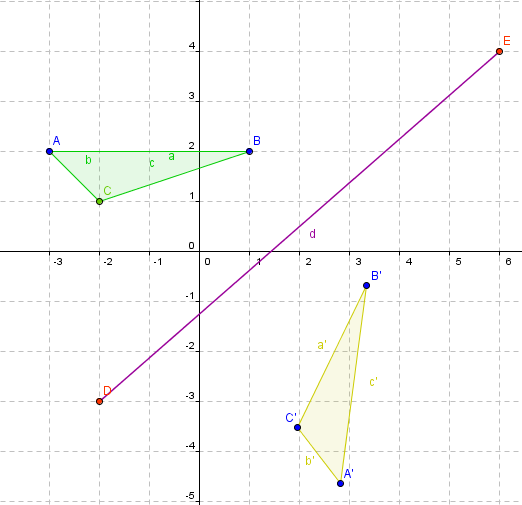
En el siguiente video puedes ver como efectuar estas transformaciones con geogebra
-
Algunas aplicaciones de la Geometria en las ártes Plásticas
Podemos integrar la geometría con otras disciplinas, específicamente con el arte plástico, pues aprenderemos a construir teselaciones, conoceremos el número pi y se profundizarán los conocimientos acerca de figuras tridimensionales -como el cono, el cilindro y la pirámide.
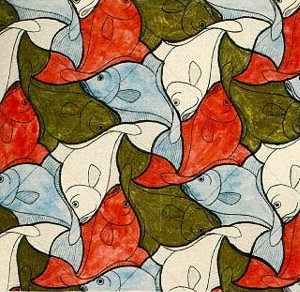
Teselación del Plano
Es la entera división del plano mediante la repetición de una o más figuras que encajan perfectamente unas con otras, sin superponerse ni dejando espacios vacíos entre ellas. Esta partición del plano suele llamarse también mosaico o embaldosado.
Por lo tanto, Embaldosar o Teselar, significa recubrir el plano con figuras que se repiten de modo que:
- Al unir las figuras se recubre completamente el plano
- La intersección de dos figuras sea vacía (sin huecos)
Existen dos tipos de teselaciones:
1) Regular: Es el recubrimiento del plano con polígonos regulares y congruentes. Son sólo tres los polígonos que se pueden utilizar: triángulo equilátero, cuadrado y hexágono regular.
Al observar éstas partes del plano embaldosadas por cada uo de los polígonos regulares. distinguimos algunas situaciones que conviene destacar:
- Al embaldosar con cuadrados, éstos se alinean perfectamente uno sobre otro; en cambio, los triángulos y hexágonos no lo hacen.
- También se observa que un hexágono regular lo forman seis triángulos equiláteros simultáneamente.
- Al cubrir un plano, ocurre en cada vértice del polígono regular, su ángulo interior debe ser divisor exacto de 360°, lo que ocurre solamente con las figuras anteriormente mencionadas.
2) Semi- Regular: Es aquella que está formada por polígonos regulares, de manera que la unión de ellos es idéntica en cada vértice. Las siguientes ocho figuras con las únicas combinaciones de polígonos regulares que permiten embaldozar completamente un plano:
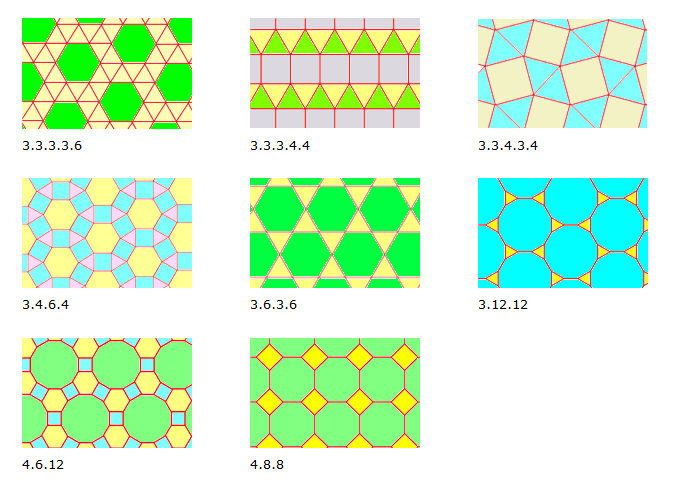
Existen otras combinaciones de polígonos regulares que aparentemente pueden cubrir el plano, pero sin embargo sólo logran cubrir el entorno del punto, es decir, no es posible extenderlas indefinidamente...
El número pi
Es la constante que relaciona el perímetro de una circunferencia con la amplitud de su diámetro: ? = L/D.
Este no es un número exacto sino que es de los llamados irracionales, ya que tiene infinitas cifras decimales.
Ya en la antigüedad, se insinuó que todos los círculos conservaban una estrecha dependencia entre el contorno y su radio, pero tan sólo desde el siglo XVII la correlación se convirtió en un dígito y fue identificado con el nombre "Pi" (de perophereia, denominación que los griegos daban al perímetro de un círculo).
-
Apertura: viernes, 13 de diciembre de 2013, 23:45Cierre: viernes, 20 de diciembre de 2013, 23:45
-
Algunas aplicaciones de la Geometria en las ártes Plásticas (Parte 2)
Si realmente te llama la atención aplicar las matemáticas al arte, puedes revisar este video, que es realmente maravilloso, sobre serie de fibonacci y número aúreo, aplicados a la naturaleza; 100% recomendado!!
Y si ésto no fué suficiente, puedes revisar ésta página, en la que muedtran las distintas áreas de la vida en la que es utilizada la Geometría:
http://www.ehowenespanol.com/aplica-geometria-arte-arquitectura-naturaleza-sobre_135302/
-
Al aprobar esta evaluación, se habilitará el sistema para la descarga del certificado. Podrás descargar cualquiera o los tres modelos de certificado en cuanto apruebas la evaluación.
-
-
Y por último, en los contenidos relativos a Primero año medio:
Trabajaremos la geometría en el plano cartesiano, donde se estudiarán las transformaciones isométricas y la congruencia de figuras. De esta manera se les presenta la oportunidad de obtener resultados geométricos y de profundizar los ya adquiridos relativos a estas transformaciones en 8° básico de manera analítica.
Específicamente, se trabajarán los elementos básicos del plano cartesiano, transformación de figuras a través de la aplicación de traslaciones, rotaciones y reflexiones, se establecen los criterios de congruencia en triángulos, y los utilizan en la resolución de problemas y en el establecimiento de propiedades en polígonos.
Contenidos
- Caracterización del plano cartesiano
- Ubicación de puntos y figuras en el plano cartesiano e identificación de las coordenadas de los vértices de polígonos dibujados en él
- Aplicación de transformaciones isométricas y composiciones de ellas en el plano cartesiano
- Concepto de congruencia
- Criterios de congruencia en triángulos
- Aplicaciones de los criterios de congruencia -
Congruencia y criterios:
En geometria se usan habitualmente los términos congruencia, equivalencia y semejanza; es por ésto que ahora haremos una distinción entre ellos:
- Dos figuras se considerarán congruentes si y solo si tienen la misma forma y tamaño.
- Dos figuras geométricas se considerarán equivalentes si tienen el mismo tamaño, es decir, áreas iguales.
- Dos figuras geométricas de diferente tamaño pero de igual número de lados se considerarán semejantes si tienen ángulos interiores congruentes y lados proporcionales.
Pero, hay postulados que establecen si dos triángulos son congruentes, sin necesidad de verificar que sus tres lados y ángulos lo sean. Por lo común, basta con asegurar tres de estos seis elementos:
Postulado LLL (lado- lado- lado)
Dos triángulos son congruentes si tienen sus tres lados respectivamente congruentes.
Postulado LAL (lado- ángulo- lado)
Dos triángulos son congruentes si tienen dos lados y el ángulo comprendido entre ellos respectivamente congruentes.
Postulado ALA (ángulo- lado- ángulo)
Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos respectivamente congruentes.
-
Final del curso: Evaluación
Bueno, espero que este curso te haya sido de mucha ayuda, y que hayas podido resolver tus dudas e inquietudes a tiempo. Ahora te dejo esta evaluación general, que evalúa todos los contenidos vistos, y servirá para que sepamos que tanto aprendiste, cuánto avanzaste y si realmente logré ayudarte... ¡Éxito!