New section
Section outline
-
Algunas aplicaciones de la Geometria en las ártes Plásticas
Podemos integrar la geometría con otras disciplinas, específicamente con el arte plástico, pues aprenderemos a construir teselaciones, conoceremos el número pi y se profundizarán los conocimientos acerca de figuras tridimensionales -como el cono, el cilindro y la pirámide.
Teselación del Plano
Es la entera división del plano mediante la repetición de una o más figuras que encajan perfectamente unas con otras, sin superponerse ni dejando espacios vacíos entre ellas. Esta partición del plano suele llamarse también mosaico o embaldosado.
Por lo tanto, Embaldosar o Teselar, significa recubrir el plano con figuras que se repiten de modo que:
- Al unir las figuras se recubre completamente el plano
- La intersección de dos figuras sea vacía (sin huecos)
Existen dos tipos de teselaciones:
1) Regular: Es el recubrimiento del plano con polígonos regulares y congruentes. Son sólo tres los polígonos que se pueden utilizar: triángulo equilátero, cuadrado y hexágono regular.
Al observar éstas partes del plano embaldosadas por cada uo de los polígonos regulares. distinguimos algunas situaciones que conviene destacar:
- Al embaldosar con cuadrados, éstos se alinean perfectamente uno sobre otro; en cambio, los triángulos y hexágonos no lo hacen.
- También se observa que un hexágono regular lo forman seis triángulos equiláteros simultáneamente.
- Al cubrir un plano, ocurre en cada vértice del polígono regular, su ángulo interior debe ser divisor exacto de 360°, lo que ocurre solamente con las figuras anteriormente mencionadas.
2) Semi- Regular: Es aquella que está formada por polígonos regulares, de manera que la unión de ellos es idéntica en cada vértice. Las siguientes ocho figuras con las únicas combinaciones de polígonos regulares que permiten embaldozar completamente un plano:
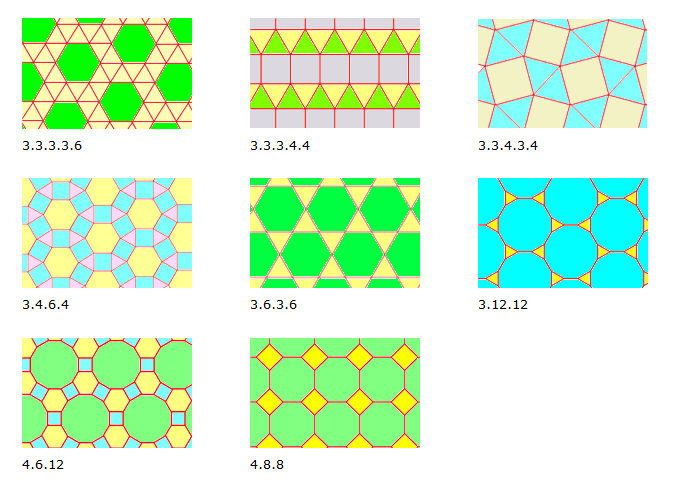
Existen otras combinaciones de polígonos regulares que aparentemente pueden cubrir el plano, pero sin embargo sólo logran cubrir el entorno del punto, es decir, no es posible extenderlas indefinidamente...

El número pi
Es la constante que relaciona el perímetro de una circunferencia con la amplitud de su diámetro: ? = L/D.
Este no es un número exacto sino que es de los llamados irracionales, ya que tiene infinitas cifras decimales.
Ya en la antigüedad, se insinuó que todos los círculos conservaban una estrecha dependencia entre el contorno y su radio, pero tan sólo desde el siglo XVII la correlación se convirtió en un dígito y fue identificado con el nombre "Pi" (de perophereia, denominación que los griegos daban al perímetro de un círculo).

-
Opened: Friday, 13 December 2013, 11:45 PMDue: Friday, 20 December 2013, 11:45 PM
